Riviere JE, Gabrielsson J, Fink M, Mochel J. 2016; Mathematical modeling and simulation in animal health. Part I: moving beyond pharmacokinetics. J Vet Pharmacol Ther 39: 213-23. PMID:
10.1111/jvp.12278. PMID:
26592724.


Gabrielsson J, Weiner D. 2016. Pharmacokinetic and pharmacodynamic data analysis: concepts and applications. . 5th ed. Apotekarsocieteten. Stockholm.
Derendorf H, Meibohm B. 1999; Modeling of pharmacokinetic/pharmacodynamic (PK/PD) relationships: concepts and perspectives. Pharm Res 16: 176-85. PMID:
10.1023/A:1011907920641. PMID:
10100300.


Holford NH, Sheiner LB. 1981; Understanding the dose-effect relationship: clinical application of pharmacokinetic-pharmacodynamic models. Clin Pharmacokinet 6: 429-53. PMID:
10.2165/00003088-198106060-00002. PMID:
7032803.


Meibohm B, Derendorf H. 1997; Basic concepts of pharmacokinetic/pharmacodynamic (PK/PD) modelling. Int J Clin Pharmacol Ther 35: 401-13. PMID:
9352388.

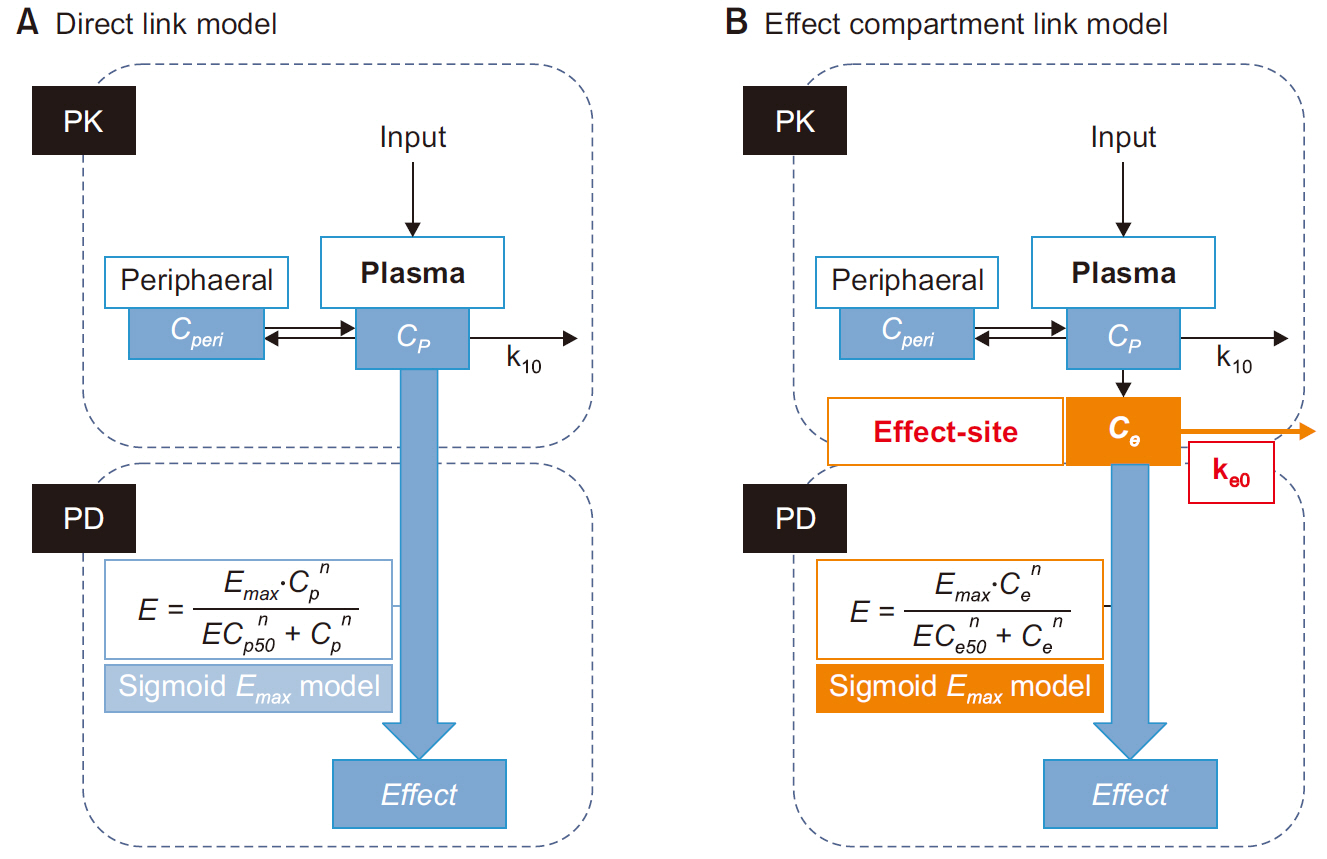
Louizos C, Yáñez JA, Forrest ML, Davies NM. 2014; Understanding the hysteresis loop conundrum in pharmacokinetic/pharmacodynamic relationships. J Pharm Pharm Sci 17: 34-91. PMID:
10.18433/J3GP53. PMID:
24735761. PMID:
PMC4332569.



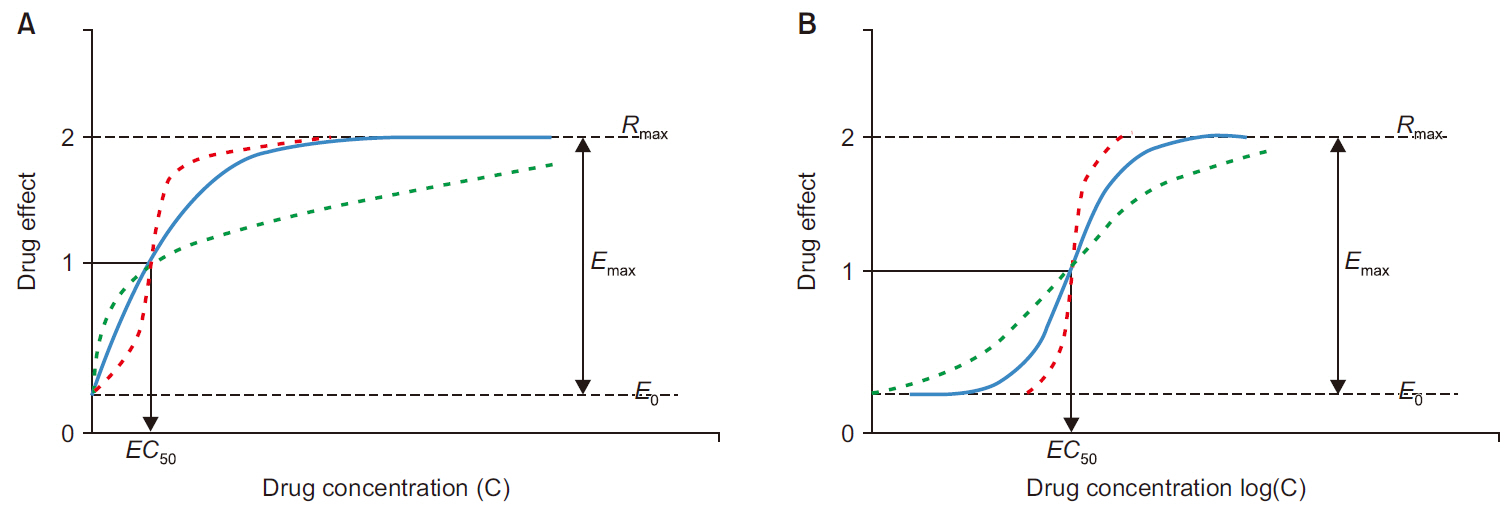
Gabrielsson J, Weiner D. In: Gabrielsson J, Weiner D, 2016. Pharmacodynamic concepts. editors. Pharmacokinetic and Pharmacodynamic Data Analysis: Concepts and Applications. 5th ed. Apotekarsocieteten. Stockholm, p. 199-332.
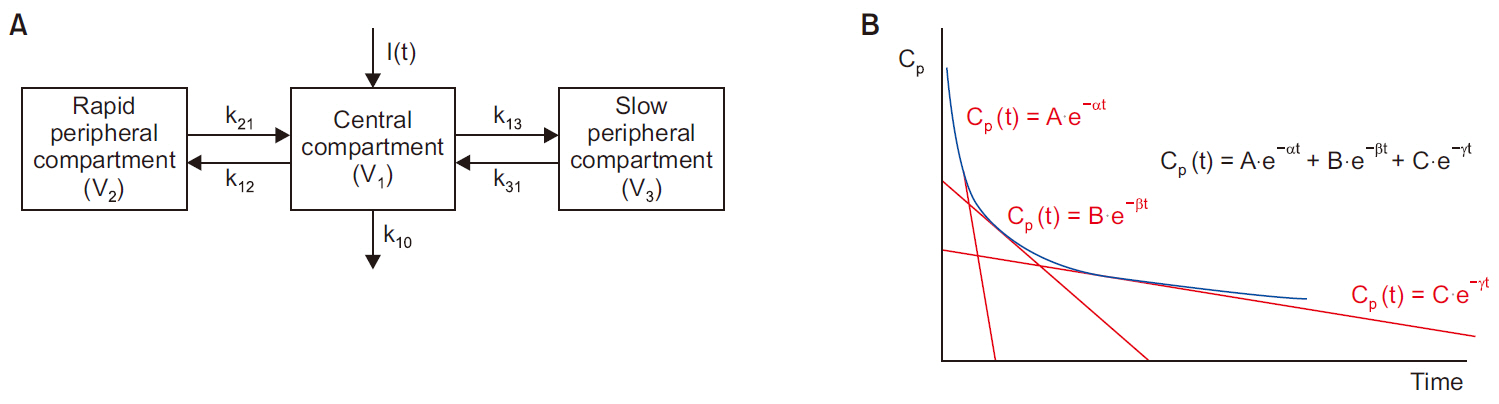
Gabrielsson J, Weiner D. In: Gabrielsson J, Weiner D, 2016. Pharmacokinetic concepts: multi-compartment model. editors. Pharmacokinetic and Pharmacodynamic Data Analysis: Concepts and Applications. 5th ed. Apotekarsocieteten. Stockholm, p. 57-72.
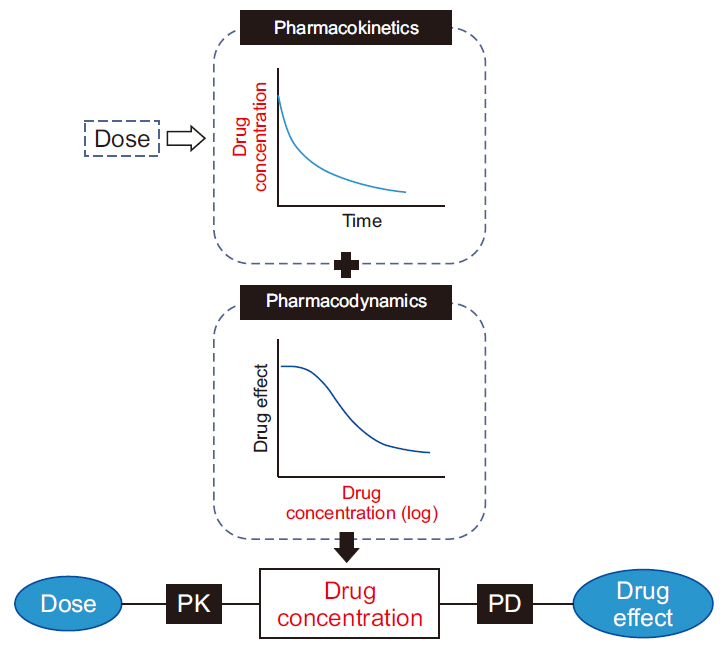
Han DW. 2014; Pharmacokinetic and pharmacodynamic modeling in anesthetic field. Anesth Pain Med 9: 77-86.
Hill AV. 1910; The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J Physiol 40: 4-7.
Crommelin DJA, Sindelar RD, Meibohm B. 2019. Pharmaceutical biotechnology: fundamentals and applications. . 5th ed. Springer. Cham, PMID:
10.1007/978-3-030-00710-2.

Sheiner LB, Stanski DR, Vozeh S, Miller RD, Ham J. 1979; Simultaneous modeling of pharmacokinetics and pharmacodynamics: application to d-tubocurarine. Clin Pharmacol Ther 25: 358-71. PMID:
10.1002/cpt1979253358. PMID:
761446.


Holford NH, Sheiner LB. 1981; Pharmacokinetic and pharmacodynamic modeling in vivo. Crit Rev Bioeng 5: 273-322. PMID:
7023829.

Segre G. 1968; Kinetics of interaction between drugs and biological systems. Farmaco Sci 23: 907-18. PMID:
5712792.

Kowalski KG, Karim A. 1995; A semicompartmental modeling approach for pharmacodynamic data assessment. J Pharmacokinet Biopharm 23: 307-22. PMID:
10.1007/BF02354287. PMID:
8834198.


Choi BM, Koh EH, Kim MG, Kim SH, Ok SY, Noh GJ. 2013; Temporal linear mode complexity as a surrogate measure of the anesthetic drug effects during sevoflurane anesthesia. Korean J Anesthesiol 65: 385-96. PMID:
10.4097/kjae.2013.65.5.385. PMID:
24363840. PMID:
PMC3866333.



Bruhn J, Röpcke H, Hoeft A. 2000; Approximate entropy as an electroencephalographic measure of anesthetic drug effect during desflurane anesthesia. Anesthesiology 92: 715-26. PMID:
10.1097/00000542-200003000-00016. PMID:
10719951.